Simulating the Schwinger effect in 1+1 dimensions on a fault-tolerant quantum computer
Key Insights
Researchers from PsiQuantum have conducted a detailed analysis of quantum resource estimates (QREs) for studying the Schwinger effect (electron-positron pair production from background electric-field energy) in 1+1 dimensions. This was done by compiling two quantum-simulation algorithms for two relevant instances that were examined: (a) the quench of the electric field where the interaction is turned on at t=0 and electron-positron pairs start getting created, and (b) the scattering/splitting of an electron-positron particle pair that then travels through the lattice.
The Schwinger effect in 1+1 dimensions is a key sandbox model used in particle physics to demonstrate relevant effects for quantum electrodynamics (QED), with the aim of studying it to use these learnings for higher-complexity models of QED and quantum chromodynamics (QCD).
Two promising Hamiltonian-simulation methods are employed to study the Schwinger effect in these instances: (i) a second-order Suzuki-Trotter formula, and (ii) truncated and discretized Dyson series that approximates the evolution in the interaction picture.
(i) is chosen because the commutator-norm scaling and the qubit requirements are more favorable with a high-energy cutoff when compared to a usual block-encoding method.
(ii) is chosen because the scaling with the high-energy cutoff is even more favorable than method (i), particularly when the Hamiltonian can be separated into two parts: one part of the Hamiltonian is large and fast-forwardable (i.e., its time evolution does not require a lot of resources to implement), while the other part is not fast-forwardable and can be treated as a perturbation of the first part, like in the interaction picture.
In both cases, the quantum circuits are fully compiled, and explicit quantum resource estimates are given for a range of values of relevant parameters: number of lattice sites, electric-field cutoff, initial electric-field strengths, and the minimum time required for the system’s evolution to the point of observing the Schwinger effect. Methods (i) and (ii) are compared to see which method gives lower QREs at which range of parameter values.
The findings indicate that method (ii) is more suitable for the studying of the Schwinger effect at the time scale and energy cutoff when it’s expected to happen because the number of operations scales more favorably: poly-logarithmically vs. linearly for the energy cutoff, showing an exponential speed-up of the interaction-picture method. Additionally, the precision also shows better scaling: logarithmic vs. square-root. The drawback is that the required number of logical qubits is somewhat higher. Given that the fully compiled algorithm circuits are provided for both methods, theoretical physicists that are interested in testing out either method can do so in different regimes. In most cases, and for both methods, the number of required logical qubits is between ~240 and ~4600, and the number of T-gates needed is between 10⁵ and 10¹³.
There are two possible next steps in the development of this research:
Expansion of the methods to higher-dimensional and more physically complete models: from a U(1) gauge field coupled to fermions in 1+1 dimensions (sandbox model) to SU(3) fields coupled to fermions in 3+1 dimensions (realistic conditions), which would make this research even more valuable for QED and QCD.
Exploring how to encode more constraints into the studied Hamiltonian, e.g., transforming it into an equivalent one where the gauge degrees of freedom are eliminated, to reduce the number of logical qubits; however, this will come at the expense of additional operations for the circuit.
Context setting: a toy model exhibiting close to real-life behaviors
The Schwinger model: quantum electrodynamics (QED) in 1+1 space and time dimensions, has a long history as a toy model for understanding phenomena in quantum field theory (QFT). The idea is that the understanding of 1+1-D behavior will lend insight into theories in higher dimensions. The Schwinger model is conceptually simpler than 3+1-D QFT theories like quantum chromodynamics (QCD), the 1+1D setting captures relevant features present in those higher-dimensional models, e.g., confinement (relevant for quarks in 3D, possible for electrons and positrons in 1D because of dimensional constraints), dynamical mass generation, and a non-perturbative vacuum structure.
It also allows the study of how electron-positron pairs can be generated from vacuum due to the presence of a strong electric field: the Schwinger effect. QFT predicts that under the right conditions, energy stored in the background field can convert into matter-antimatter pairs. While the Schwinger model is analytically solvable in the continuum limit for constant background fields and massless fermions, studying it in more realistic cases, e.g., with fluctuating fields and massive fermions, requires numerical simulation. Using numerics also requires the discretization of space, introducing a lattice to the system.
Unfortunately, simulation methods on classical computers hit hard limits in regimes that are interesting for study:
Tensor network techniques (such as matrix product states) can simulate ground states and short-time dynamics, but they struggle with the growth of entanglement and real-time evolution.
Monte Carlo approaches struggle with simulating quantum interference due to the sign problem: interpreting complex amplitudes, which can take positive and negative values, as probabilities leads to massive noise in the signal that ends up requiring an exponential number of samples to resolve.
Novel research
That is where fault-tolerant quantum simulation comes in. Researchers at PsiQuantum have conducted a detailed quantum resource estimate (QRE) analysis for simulating the Schwinger model on fault-tolerant quantum computers. The study focuses on two scenarios involving dynamics:
(a) a quench, where the interaction is switched on at time t=0, triggering pair production from vacuum, and
(b) scattering/splitting, where an existing particle–antiparticle pair propagates through the lattice and interacts with the field.
What sets this work apart is the end-to-end compilation of these simulations into explicit quantum circuits which allowed researchers to calculate QREs across physically relevant parameter ranges for two algorithmic methods for Hamiltonian simulation:
(i) a second-order Suzuki–Trotter product formula, and
(ii) a truncated, discretized Dyson-series algorithm in the interaction picture
Method (i) was selected because it benefits from three key advantages in this context. Firstly, the scaling of the commutator-norm error is favorable for lattice-local Hamiltonians like in the Schwinger model. Secondly, the qubit overhead is lower, making this method potentially better suited for early-stage fault-tolerant hardware with fewer logical qubits. In the implementation, the Hamiltonian is separated into the electric field, mass, and interaction terms, and the evolution is ordered in such a way as to minimize error buildup. Thirdly, it can handle the high electric-field cutoff better than the frequently used block-encoding approach.
Method (ii) approximates time evolution by expanding the Dyson series of the interaction term, using a separation of the Hamiltonian into H = H₀ + V, where:
H₀ (electric field + mass terms) is large and fast-forwardable, i.e., it can be simulated efficiently at long time scales, and
V (interaction term) is treated as a perturbation.
This method is analytically attractive because its cost scales with the size of the perturbation term V, not the full Hamiltonian. Importantly, the scaling with the electric-field cutoff Λ is exponentially improved: while the Trotter method’s gate cost scales linearly with Λ, the interaction-picture method scales poly-logarithmically as (log Λ)². Similarly, the dependence on precision ε is better: log (1/ε) versus the square-root 1/√ε scaling of method (i). The drawback is that the required number of logical qubits is somewhat higher. In most cases, and for both methods, the number of required logical qubits is between ~240 and ~4600, and the number of T-gates needed is between 10⁵ and 10¹³.
Comparison between the Product-Formula and the Interaction-Picture methods
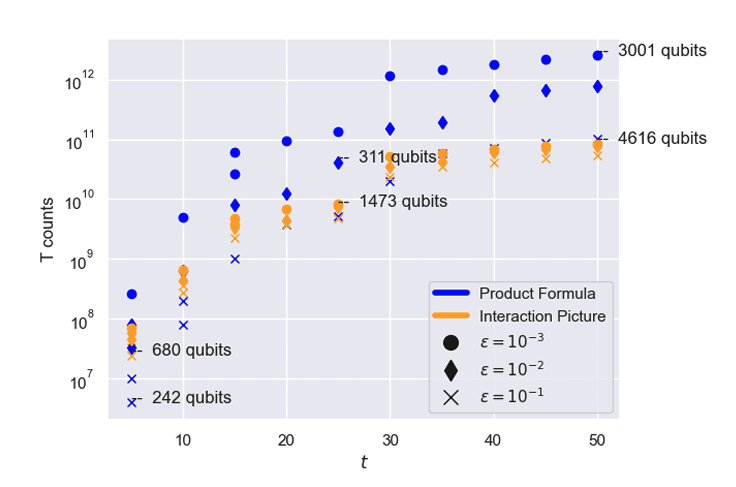
Figure 1: QRE comparison between the best implementations of the Product-Formula (blue) and the Interaction-Picture (orange) methods (methods (i) and (ii) in the text, respectively) for a range of allowed simulation errors ε (0.1, 0.01 and 0.001) in the weak-coupling regime requiring a longer time evolution to observe the Schwinger effect. The qubit counts for method (i) are lower (from 242 to 3001 qubits) than for method (ii) (from 680 to 4616 qubits); however, the required number of T-gates to simulate longer evolution is higher by approximately an order of magnitude (~10¹² vs. 10¹¹ T-gates).
Conclusion: a laid-out path for how to study the Schwinger model on a fault-tolerant quantum computer
This study helps in positioning the Schwinger model as a concrete testing ground for benchmarking quantum-simulation algorithms. By grounding their analysis in two physically motivated scenarios: (a) real-time field quench, and (b) particle scattering, the PsiQuantum team has provided the community with fully compiled quantum circuits and concrete resource counts using two different Hamiltonian-simulation methods.
That level of detail and completeness is what makes this work stand out. Rather than stopping at asymptotic complexity, the researchers compiled both simulation methods all the way down to Clifford + T circuits, quantified the required auxiliary qubits, and calculated fault-tolerant resource estimates across a wide range of physically relevant parameters. This allows for a direct comparison of algorithm performance in regimes where the Schwinger effect is observable.
When it comes to the simulation methods used, both have their place. The Suzuki–Trotter approach is more qubit-efficient and remains effective in lower-cutoff or short-time regimes, making it appealing for early fault-tolerant quantum hardware. The interaction-picture Dyson-series method, on the other hand, becomes the better choice at high field cutoffs, long evolutions, or tight error budgets. It offers exponential scaling improvements in both cutoff and precision at the cost of a higher qubit count.
What’s next?
This work establishes a foundation for simulating real-time gauge-theory dynamics on fault-tolerant quantum hardware, with two possible directions for future research:
Dimension scaling to 3+1: while the Schwinger model in 1+1 dimensions offers a tractable and insightful sandbox, scaling up to 3+1 dimensions would move the research closer to simulating full QED or QCD under realistic conditions. While such an extension introduces new challenges, e.g., more complex gauge structures, i.e., going from U(1) to SU(3), different field behavior due to increased dimensionality, and additional particle types, it would expand the relevance of these simulation techniques for high-energy physics.
Optimization of qubit counts through physics encoding: there is room to optimize the qubit requirements by incorporating more physical constraints directly into the Hamiltonian encoding, e.g., transforming the Hamiltonian to an equivalent one where the gauge degrees of freedom are eliminated. However, this will come at the cost of more complicated Hamiltonian terms to implement.
Together, these directions point toward a broader agenda: refining both the physical modeling and the algorithmic engineering needed to make fault-tolerant quantum simulations of fundamental physics a reality.
Essential Terms
Confinement: phenomenon where the force between charged particles increases with the distance between them. As a result, the force pushes the particles together and prevents the observation of isolated charges; only bound, neutral combinations, e.g., quark–antiquark or electron-positron pairs, are observable.
Schwinger effect: creation of matter–antimatter pairs from vacuum when a strong background electric field provides enough energy for this to happen.
Dyson series: time-ordered expansion of the interaction Hamiltonian that expresses the full time evolution, which often cannot be evaluated exactly, as a sum over integrals of simpler interaction terms. This allows one to approximate complex dynamics.